KCL چیست؟ Kirchhoff's Current Law
در این آموزش، نگاهی به KCL یعنی (قانون جریان Kirchhoff) خواهیم انداخت. KCL یک قانون اولیه برای مدارهای الکتریکی است. در سال 1845، گوستاو روبرت کیرشهوف، فیزیکدان آلمانی، دو قانون اساسی برای حل مدارهای الکترونیکی ارائه کرد. اولی KVL (قانون ولتاژ Kirchhoff) و دومی KCL (قانون جریان Kirchhoff). این قوانین کیرشهوف جانشین قانون اهم هستند که توسط جورج اهم ارائه شد و پس از آن معادله ماکسول توسط جیمز ماکسول ارائه شد. هر دوی این قوانین نقش بسیار مهمی در حل مدارهای مختلف در پروژه های مهندسی دارند. این قوانین همچنین برای محاسبات فرکانس و زمان مفید هستند. قوانین Kirchhoff نه تنها برای مدارهای DC قابل اجرا هستند، بلکه برای مدارهای AC، زمانی که تشعشعات الکترومغناطیسی دارای مقادیر فرکانس بالایی هستند، کار می کنند. به زبان ساده، KCL می گوید که مجموع جریان وارد شده به یک نقطه (گره) از مدار همیشه برابر با صفر است. با در این مقاله نگاهی به معرفی، کارکرد، کاربردها و سایر پارامترهای KCL خواهیم داشت.
KCL چیست (قانون جریان Kirchhoff)
KCL (قانون ولتاژ Kirchhoff)، همچنین به عنوان قانون اول Kirchhoff شناخته می شود، توضیح می دهد که مجموع جریان های وارد شده به یک گره از مدار همیشه برابر با صفر است. به بیان دیگر این قانون توضیح می دهد که جریانی که به نقطه ای از مدار وارد می شود برابر با جریانی است که از آن نقطه در مدار خارج می شود.
KCL همچنین به عنوان قانون پایستگی بار نامیده می شود زیرا جریان در نقطه اشتراک مدار ذخیره می شود که به این معنی است که در یک نقطه جریان از بین نمی رود.
قانون جریان Kirchhoff برای اندازه گیری جریان در شاخه های مختلف هر مدار استفاده می شود. این موضوع را اکنون در یک مدار ساده را توضیح می دهیم.
در مدار داده شده می بینید که شش شاخه وجود دارد که به نقطه مشترک متصل می شوند، این نقطه مشترک به عنوان گره نیز شناخته می شود.
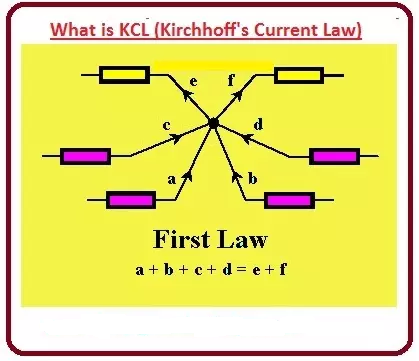
در این مدار جهت جریان در این شش شاخه با a، b، c، d، e و f نشان داده می شود.
همانطور که قبلاً بحث کردیم، KCL میگوید جریانی که به یک نقطه میآید مثبت تلقی شود و جریان خارج شونده منفی در نظر گرفته شود. می توانید در مدار ببینید که جریان های (a، b، c، d) به سمت نقطه مشترک می آیند، بنابراین این جریان ها مثبت و جریان (e، f) با دور شدن از نقطه منفی محسوب می شوند.
اگر KCL را به این مدار اعمال کنیم، معادله زیر حاصل خواهد بود.
a+b+c+d=e+f
عملکرد KCL (قانون جریان کیرشهوف)
اکنون در مورد نحوه عملکرد این قانون بحث می کنیم و مدار ساده زیر را توضیح می دهیم.
در این مدار می بینیم که یک گره وجود دارد که چهار سیم به آن متصل است، جریان از هر سیم عبور می کند.
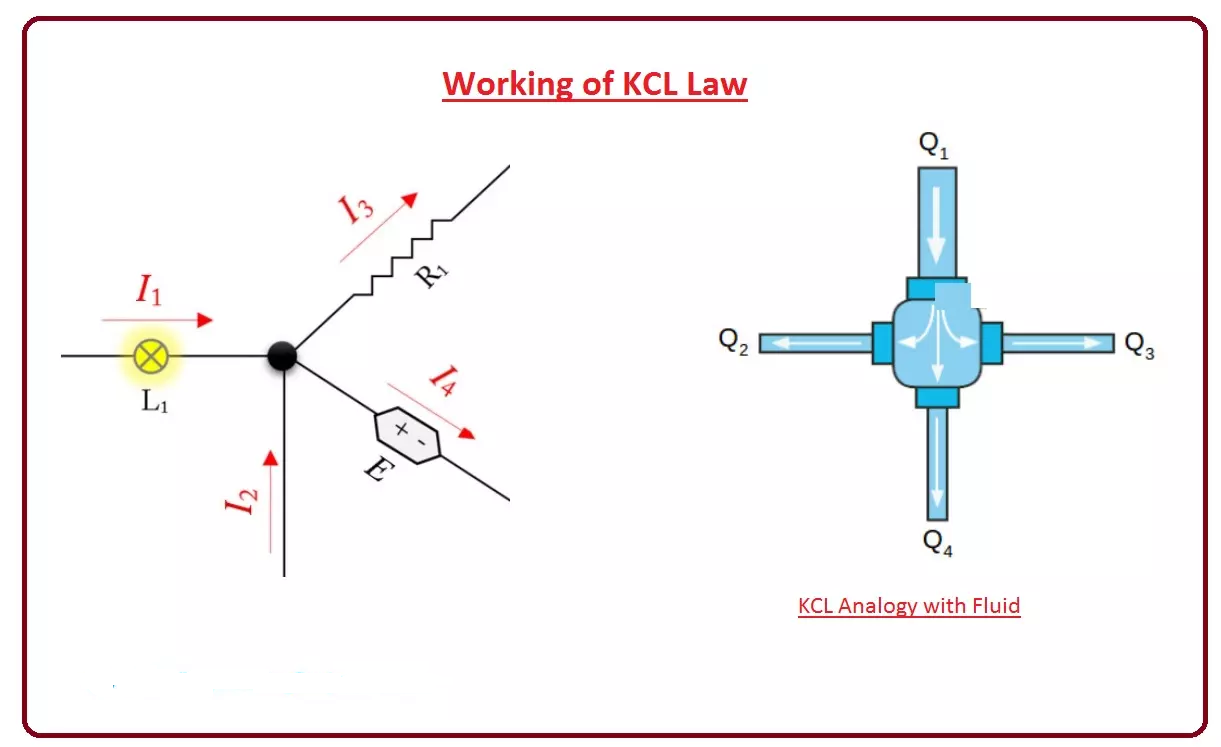
اگر KCL را به مدار اعمال کنیم، معادله این مدار است
(I1)+(I2)–(I3)–(I4)=0
این معادله را همچنین می توانید برای توصیف جریان وارد شونده به گره و جریان خارج شونده از گره بنویسد.
(I1)+(I2)=(I3)+(I4)
این معادله نشان می دهد که (I1) و (I2) به سمت گره می آیند و (I3) و (I4) از گره دور می شوند.
برای درک آسان این قانون، این مدار داده شده را با مدار مایع مرتبط می کنیم.
فرض کنید لوله ای داریم که در آن مایع با سرعت جریان (Q1) در حال حرکت است.
اگر این لوله را به 3 لوله کوچکتر تقسیم کنیم، سرعت جریان مایعی که می آید برابر با دور شدن مایع از نقطه مرکزی خواهد بود. برای درک بیشتر، نموداری از این مدار مایع را می بینیم که شبیه به KCL است.
(Q1) = (Q2) + (Q3) + (Q4)
تحلیل گره ای
این روش از KCL برای یافتن مقدار ولتاژ در گره و سپس محاسبه مقادیر جریان و ولتاژ در هر جزء مدار استفاده میکند.
برای اعمال این قانون باید مراحلی را دنبال کنید که در زیر توضیح داده شده است.
برای اعمال این قانون، اول از همه، باید تعداد گره ها را در مدار و گره مرجع پیدا کنید.
سپس جریان و مسیر آن را به هر (شاخه) گسسته مدار اختصاص دهید.
KCL را به هر گره مدار اعمال کنید.
سپس معادلاتی ایجاد کنید و آنها را حل کنید تا مقادیر جریان (I) و ولتاژ (V) را پیدا کنید.
سپس مقادیر جریان (I) و ولتاژ (V) را در هر جزء مدار پیدا کنید.
مثالی از تحلیل گره ای
اکنون در مورد اینکه چگونه تحلیل گره ای به صورت عملی کار می کند و چه رابطه ای با KCL دارد بحث می کنیم.
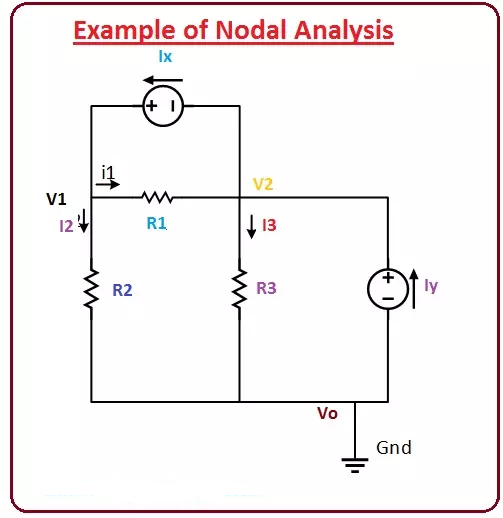
مفروضات مساله در اینجا آورده شده است.
منبع جریان (Ix) = (5 آمپر)
منبع فعلی (Iy) = (10 آمرز)
مقاومت (R1) = (4 اهم)
مقاومت (R2) = (2 اهم)
مقاومت (R3) = (6 اهم)
اول از همه، گره مرجع را در این مدار پیدا می کنیم، V0 را به عنوان یک گره مرجع در نظر می گیریم زیرا به ترمینال زمین متصل است.
همانطور که می دانیم پتانسیل زمین صفر است، بنابراین محاسبه ما را ساده می کند.
می توانید ببینید که سه گره در این گره وجود دارد که اولی (V1)، دومی (V2) و سومی V0 است که گره مرجع ما است.
اکنون از KCL روی گره (V1) و گره (V2) برای یافتن معادلات آنها استفاده می کنیم.
معادله گره اول به صورت زیرخواهد بود.
(Ix) = (I1 + I2)
(Iy)= (I3 - I1)
اکنون مقادیر عناصر شناخته شده مدار را قرار می دهیم.
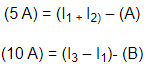
از شکل می بینید که سه جریان مجهول در این مدار در حال حرکت است (I1, I2, I3) که از قانون اهم برای یافتن معادلات آنها استفاده می کنیم.
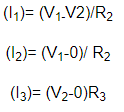
حال این مقادیر فعلی را در معادله A و B قرار می دهیم.
ابتدا این مقادیر را در رابطه A قرار می دهیم.
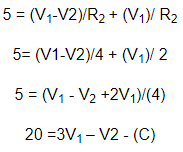
حال مقادیر (I1,I2,I3) را در رابطه B قرار داده و معادله حاصل را می سازیم.
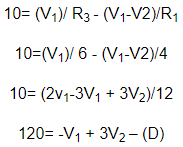
با حل معادلات C و D مقادیر V1 و V2 را داریم.
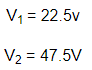
اکنون از این مقادیر استفاده می کنیم و (I1,I2,I3) را پیدا می کنیم.
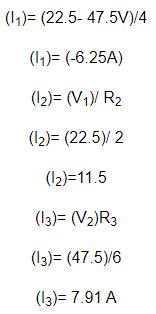
کاربردهای قانون KCL
KCL برای یافتن پارامترهای الکتریکی مختلف مانند جریان، ولتاژ و مقاومت در مدارهای مختلف استفاده می شود اما بیشتر در مدارهای پیچیده برای یافتن پارامترهای الکتریکی استفاده می شود.



دیدگاه خود را بنویسید