KVL چیست؟ Kirchhoff's Voltage Law
در این آموزش، نگاهی به KVL یعنی (قانون ولتاژ Kirchhoff) خواهیم انداخت. KVL یک قانون اولیه برای مدارهای الکتریکی است. در سال 1845، گوستاو روبرت کیرشهوف، فیزیکدان آلمانی، دو قانون اساسی برای حل مدارهای الکترونیکی ارائه کرد. اولی KVL (قانون ولتاژ Kirchhoff) و دومی KCL (قانون جریان Kirchhoff). این قوانین کیرشهوف جانشین قانون اهم هستند که توسط جورج اهم ارائه شد و پس از آن معادله ماکسول توسط جیمز ماکسول ارائه شد. هر دوی این قوانین نقش بسیار مهمی در حل مدارهای مختلف در پروژه های مهندسی دارند. این قوانین همچنین برای محاسبات فرکانس و زمان مفید هستند. قوانین Kirchhoff نه تنها برای مدارهای DC قابل اجرا هستند، بلکه برای مدارهای AC، زمانی که تشعشعات الکترومغناطیسی دارای مقادیر فرکانس بالایی هستند، کار می کنند. به زبان ساده، KVL می گوید که مجموع ولتاژها در یک مدار حلقه بسته همیشه برابر با صفر است. با استفاده از این قانون به راحتی می توانیم پارامترهای مختلف مدار مانند مقاومت، جریان یا ولتاژ را به راحتی پیدا کنیم. در این مقاله نگاهی به معرفی، کارکرد، کاربردها و سایر پارامترهای KVL خواهیم داشت.
KVL چیست (قانون ولتاژ Kirchhoff)
KVL (قانون ولتاژ Kirchhoff)، همچنین به عنوان قانون دوم Kirchhoff شناخته می شود، توضیح می دهد که مجموع ولتاژها در مدار بسته همیشه برابر با صفر است.
KVL برای اندازه گیری ولتاژ در مدارها اعمال می شود. برای توضیح آن، مدارهای داده شده را مورد بحث قرار می دهیم.
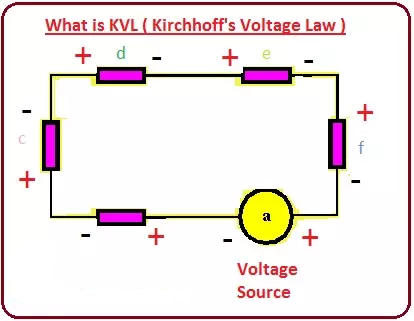
همانطور که در یک مدار مشخص می بینید که منبع تک ولتاژ با عناصر غیرفعال (منظور از عنصر الکتریکی پسیو عنصری است که مانند یک مقاومت توان تولید نمی کند) که دارای ولتاژ (b,c,d,e,f) هستند مرتبط است.
از آنجایی که همه این عناصر به صورت سری به هم متصل می شوند، مقادیر ولتاژ با هم جمع می شود.
بنابراین، مجموع همه ولتاژها در تمام اجزای مدار همیشه برابر با 0 است.
a+b+c+d+e+f=0
تحلیل مش چیست؟
این روشی است که به ما کمک می کند تا جریان و ولتاژ را در هر حلقه نزدیکی که با KVL کار می کند، پیدا کنیم، با این تجزیه و تحلیل می توانیم مقادیر جریان و ولتاژ را در هر جزء از حلقه در مدار پیدا کنیم.
سه مرحله برای اعمال این تحلیل مش وجود دارد. که در اینجا توضیح داده شده است.
مقادیر جریان گسسته را به هر دایره محصور در شبکه اختصاص دهید.
پس از آن قانون ولتاژ Kirchoff را در مورد هر دایره محصور سیستم اعمال کنید.
و معادلات خطی همزمان حاصل را حل کنید تا مقدار جریان در حلقه را بیابید.
مثال برای تحلیل مش
اکنون با مثال داده شده عملاً تحلیل مش را مورد بحث قرار می دهیم.
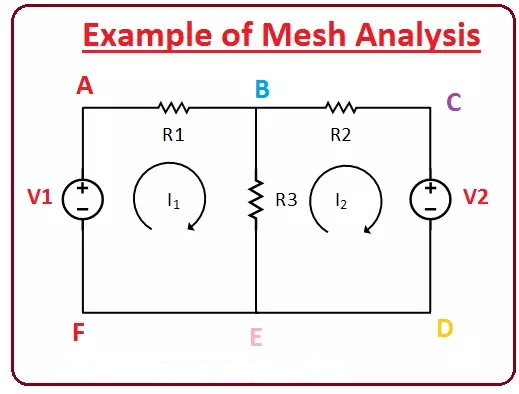
فرض کنید که یک مدار مانند شکل زیر داریم که دارای دو حلقه است و باید قانون مش را روی این مدار اعمال کنیم.
مقادیر اجزای بکار رفته در این مدار در زیر آورده شده است.
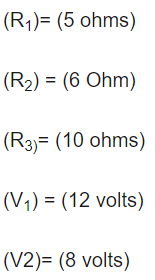
برای اعمال قانون مش روی این مدار، ابتدا جهت جریان در این دو حلقه را تشخیص می دهیم.
در حلقه اول که (ABEF) است جهت جریان در جهت عقربه ساعت است و به صورت (I1) نمایش داده می شود.
در حلقه دوم که (BCDE) است جهت جریان (I2) نیز در جهت عقربه های ساعت است.
حالا با استفاده از kVl معادله هر دوی این دو حلقه را بنویسید.
![]()
این معادله را می توان به صورت هم نوشت
![]()
حال اگر KVL را در حلقه 2 اعمال کنیم، این معادله را به صورت زیر داریم.
![]()
می توان معادله بالا را به صورت هم نوشت
![]()
اکنون مقادیر پارامترهای داده شده مدار را قرار داده و مقدار پارامتر مجهول را پیدا می کنیم.
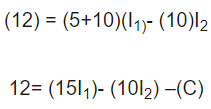
وقتی در معادله B مقدار را قرار دهیم، داریم:
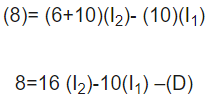
با حل معادله C و D داریم.
![]()
![]()
مثالی از KVL (قانون ولتاژ Kirchhoff)
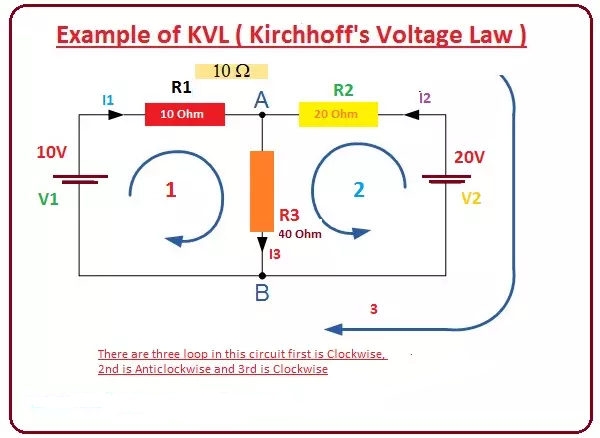
در مدار رسم شده در زیر قصد داریم KVL را در آن اعمال کنیم.
در این مدار، سه حلقه وجود دارد که در مدار با شماره های 1، 2، 3 مشخص شده اند.
KVL را یکی یکی روی این سه حلقه اعمال می کنیم و معادلات متناظر به دست می آوریم.
وقتی KVL را به حلقه اول اعمال می کنیم، این معادله را به دست می آوریم.
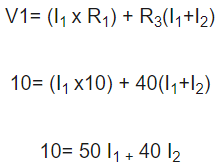
پس از اعمال KVL در حلقه اول، اکنون آن را در حلقه دوم اعمال می کنیم سپس معادله ای برای این حلقه به دست می آوریم.
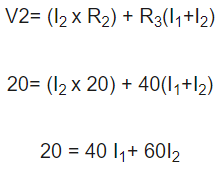
پس از یافتن معادلات حلقه اول و دوم، اکنون معادله حلقه سوم را پیدا می کنیم.
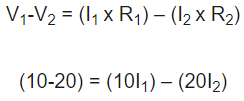
با حل معادلات حلقه یک و دوم مقدار (I1) و (I2) را بدست می آوریم که در زیر به آنها اشاره می شود.
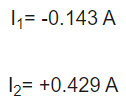
با استفاده از مقدار I1 و I2 اکنون مقدار I3را پیدا می کنیم.
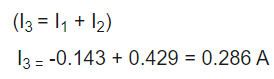
I3 جریانی است که از مقاومت (R3) می گذرد، همچنین می توانیم مقدار ولتاژ این مقاومت را با استفاده از I3 پیدا کنیم.
![]()
کاربردهای قانون KVL
قوانین Kirchhoff برای اندازه گیری استانداردهای ناشناخته مانند جریان (I)، ولتاژ (V) و همچنین جهت حرکت جریان در مدار استفاده می شود.
این قانون برای هر مداری قابل اجرا است اما برای حل مدارهای پیچیده بسیار مفید است.
این قانون همچنین به ما کمک می کند تا انتقال قدرت را در مدار مشاهده کنیم.



دیدگاه خود را بنویسید