آشنایی با سلف (Inductance)

سلام دوستان امیدوارم حالتون عالی باشه. در این مقاله قصد داریم شما را با سلف (بوبین یا اندوکتانس) آشنا کنیم. در سال 1886 اولین بار واژه اندوکتانس توسط دانشمند انگلیسی الیور هیوساید استفاده شد. نماد اندوکتانس L است که به خاطر دانشمندی به نام هاینریش لنز که قانون معروف لنز را ارائه کرد نامگذاری شد. در سیستم بین المللی (SI) واحد اندوکتانس هنری است. می توان آن را به گونه ای تعریف کرد که اگر یک ولت به سیم پیچ داده شود و جریان 1 آمپر از سیم پیچ عبور می کند تا شار القا شده در سیم پیچ یک وبر باشد، اندوکتانس سیم پیچ یک هانری خواهد بود. نام هنری به دلیل دانشمند آمریکایی جوزف هنری است که پدیده های خود القایی را کشف کرده است. در این مقاله نگاهی به پارامترهای مختلف اندوکتانس و عملکرد آن خواهیم داشت. 

سلف یا همان اندوکتانس چیست

اندوکتانس خاصیت هر هادی است به این دلیل که در برابر هر گونه تغییر در جریان عبوری از خود مقاومت می کند.

جریان عبوری از هادی میدانی را در اطرف آن ایجاد می کند، بزرگی میدان به شدت جریان بستگی دارد.

تغییر در بزرگی میدان، با تغییر در جریان، emf را در عنصر رسانا ایجاد می کند، این emf در برابر ولتاژی که جریان را تغییر می دهد مقاومت می کند.

اندوکتانس همچنین می تواند نشان دهد که مضرب نسبت ولتاژ تولیدی با تغییر در جریان است.

V = -L(di/dt)

اندوکتانس دو نوع است اولی خود القایی و دومی القایی متقابل.

اگر جریانی که از هر سلف عبور می کند، ولتاژی را در آن هادی القا کند، به عنوان خود القایی شناخته می شود.

اگر ولتاژ در هادی دوم که به هادی اول نزدیکتر است القا شود، این پدیده به عنوان القای متقابل شناخته می شود.

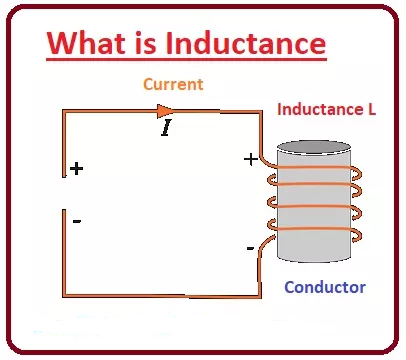
خود القایی

هنگامی که جریان از طریق جریان ولتاژ القایی در آن هادی عبور می کند، به عنوان خود القایی شناخته می شود.

L =N(ø/I)

در این معادله

L خود القایی هادی است.

N تعداد دور سیم پیچ است.

ø شار است.

I جریانی است که از هادی عبور می کند.

با توجه به شار القا شده در آن هادی، تغییرات جریان نیروی محرکه در این هادی ایجاد می کند.

با توجه به این نیروی محرکه الکتریکی، جریان دیگری در جهت معکوس جریان تامین شده توسط منبع تغذیه خارجی تولید می شود.

تغییر در این جریان در برابر تغییر در جریان اولیه مقاومت می کند.

اگر مقدار جریان اولیه در حال افزایش باشد، جریان ثانویه در برابر افزایش جریان اولیه مقاومت می کند.

اثر کلی این امر به حداقل رساندن مقدار جریان متناوب در سلف و همچنین حذف دامنه ولتاژ اعمال شده به هادی است.

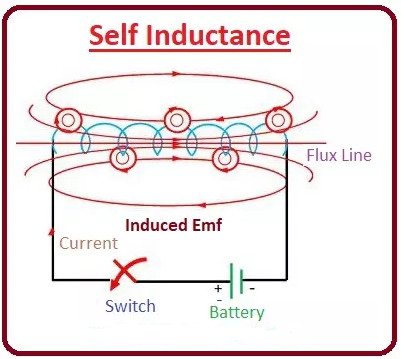
القای متقابل

اگر جریان از یک سیم پیچ عبور کند و شار آن به سیم پیچ دوم نزدیک به سیم پیچ اول القا شود، به دلیل تغییر ولتاژ شار القا شده در سیم پیچ دوم، این پدیده به عنوان القای متقابل شناخته می شود.

برای درک عملی القای متقابل، شکل داده شده زیر را مورد بحث قرار دهیم.

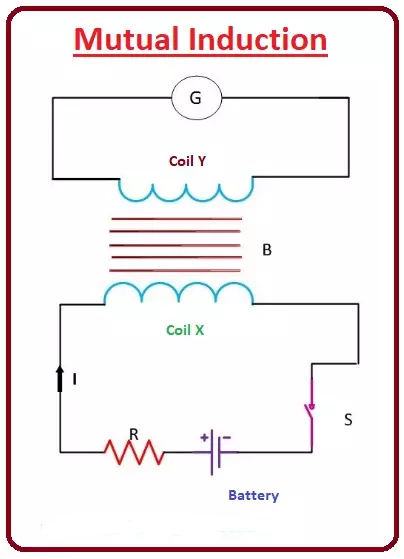
دو سیم پیچ X و Y وجود دارد که نزدیک به یکدیگر قرار دارند. هنگامی که سوییچ S را می بندیم، جریان از سیم پیچ X  عبور کرده و ولتاژی را در سیم پیچ القا می کند.

شار سیم پیچ نیز با سیم پیچ Y متناسب است، اگر جریان را در سیم پیچ X تغییر دهیم، تغییرات شار در سیم پیچ دوم نیز وجود خواهد داشت که ولتاژی را در سیم پیچ القا کرده است که به دلیل پدیده القای متقابل است.

اکنون به صورت ریاضی مقدار القای متقابل را در دو سیم پیچ پیدا می کنیم.

E_m = M (dI₁/dt)

معادله M = (E_m)/ (dI₁/dt)------(A)

این معادله زمانی استفاده می شود که مقدار ولتاژ القایی در سیم پیچ دوم را بدانیم و تغییر جریان در سیم پیچ اول مشخص باشد.

اگر مقدار یک ولت را داشته باشیم و (dI₁/dt) نیز یک آمپر باشد، با اضافه کردن این مقادیر به معادله (A)، اندوکتانس متقابل را پیدا می کنیم که یک هنری است.

از معادله داده شده در بالا، می‌توانیم اندوکتانس متقابل را به این صورت توضیح دهیم، اگر یک ولت به سیم پیچ اول ارائه شود و جریان عبوری از سیم پیچ دوم با سرعت یک آمپر در ثانیه باشد، آن‌گاه اندوکتانس متقابل یک هنری دارد.

القای متقابل را نیز می توان با این معادله توصیف کرد.

E_m = M(dI₁/dt)= d/dt (MI₁)--- (B)

E_m =N₂(dØ₁₂/dt)= d/dt (N₂Ø₁₂)---(C)

با استفاده از معادله B و C داریم.

MI₁ = N₂Ø₁₂

M = (N₂Ø₁₂ /I₁)

معادله القای متقابل در بالا فقط زمانی می تواند کار کند که برهمکنش شار با سیم پیچ دوم (N₂f₁₂) ناشی از جریان (I₁) سیم پیچ اول از قبل مشخص باشد.

از معادله القاء متقابل بالا، می توان نتیجه گرفت که M به عوامل زیر بستگی دارد.

تعداد پیچ ها در سیم پیچ دوم.

مساحت سیم پیچ ها.

فاصله بین سیم پیچ ها.

انرژی ذخیره شده در سلف

اکنون در مورد پدیده ذخیره انرژی در سیم پیچ القایی بحث می کنیم.

انرژی ذخیره شده در سلف به شکل میدان مغناطیسی.

میدان سلف مستقیماً با جریان اعمال شده به سلف متناسب است.

فرمول زیر انرژی ذخیره شده در سلف را به شکل میدان مغناطیسی توضیح می دهد.

E = 1/2 LI²

در این معادله

E مقدار انرژی ذخیره شده در سلف است.

L خود القایی هادی است.

I جریانی است که از آن هادی عبور می کند.

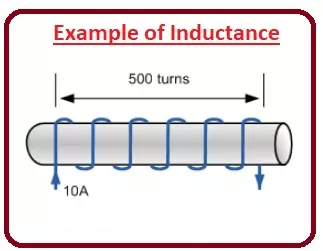
مثالی از اندوکتانس

در شکل داده شده، سیم پیچ ها با پانصد دور  از جنس مس پیچیده شده است.

وقتی ده آمپر جریان dc به سیم پیچ ها اعمال می کنیم، شار ده میلی وبر در آن سیم پیچ ایجاد می شود. اکنون مقدار خود القایی را می یابیم.

همانطور که می دانیم فرمول خود القایی به صورت زیر است.

L =N (Ø/I)

اگر مقادیر تعداد دور، شار و جریان را قرار دهیم، مقدار اندوکتانس خواهیم داشت.

=500x (0.01/10) 

 500milli-henry=