مقاومت ها در ترکیب سری شده
در این آموزش، در مورد مقاومت ها با ترکیب سری شده با هم بحث خواهیم کرد. در مهندسی برق و الکترونیک، 2 روش اصلی برای اتصال قطعات وجود دارد. اولی ترکیب سری و دومی ترکیب موازی است. اگر قطعات به صورت سری به هم متصل شوند، جریان مشابهی در همه آنها جریان می یابد اما ولتاژ دو طرف آنها متفاوت خواهد بود. مجموع افت ولتاژ در هر قطعه برابر با کل ولتاژ اعمال شده خواهد بود. در حالی که در صورت اتصال موازی ولتاژ هر عنصر یکسان بوده و جریان در هر قطعه متفاوت خواهد بود. در این مقاله، مدارهایی را مورد بحث قرار خواهیم داد که از مقاومت به صورت سری تشکیل شده اند و مقدار جریان و ولتاژ را در هر مقاومت پیدا می کنیم.
مداری که مقاومت ها را در یک خط پشت سر هم به هم متصل می کند مدار مقاومت سری نامیده می شود.
در این روش از اتصالات مقاومتی، مقدار جریان در هر مقاومت یکسان می ماند.
در شکل داده شده می بینید که جریان در هر مقاومت یکسان خواهد بود.
IR1=IR2=IR3=1mA
در این مدار داده شده 3 مقاومت به صورت سری به هم وصل شده اند، یعنی R1، R2، R3.
از آنجایی که مدار دارای ترکیبی سری از مقاومت است، برای بدست آوردن مقاومت کلی مدار، تمام این 3 مقاومت را با هم جمع می کنیم.
Rt = R1 + R2 + R3
اگر مقادیر این مقاومت ها را در معادله بالا قرار دهیم، مقاومت معادل مدار را به دست خواهیم آورد.
Req = 2O + 3O + 5O = 10O
بنابراین مقاومت معادل مدار ده اهم خواهد بود، همچنین می توان آن را به عنوان مقاومتی که می توان به جای تمام مقاومت های مدار اضافه کرد، به عنوان مقاومت معادل مدار تعریف کرد.
عبارت نهایی برای یافتن مقاومت خالص مدار به صورت داده شده است.
Rt = Rx + Ry + Rz + ….. Rn
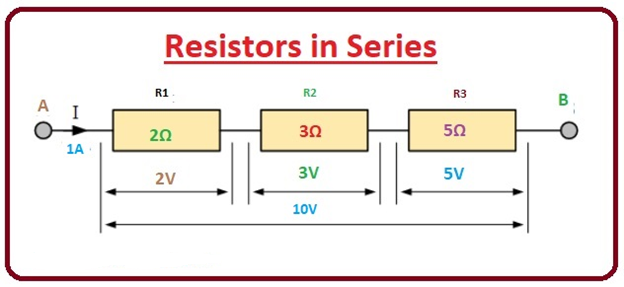
ولتاژ در ترکیب سری شده مقاومت ها
در مدار داده شده در بالا، می توانیم ببینیم که مقدار ولتاژ در هر مقاومت با سایر مقاومت ها متفاوت است. به این دلیل است که افت ولتاژ در هر مقاومت به دلیل تفاوت مقدار مقاومت ها متفاوت است.
ما می توانیم ولتاژ کل در پایانه های A و مدار را با فرمول داده شده پیدا کنیم.
Vt = VR1 + VR2 + VR3 = 10 ولت
اگر قانون اهم را برای هر مقاومت اعمال کنیم، میتوانیم مقدار ولتاژ هر مقاومت را پیدا کنیم.
VR1 = I x R1 = 1A x 2O = 2V
VR2 = I x R2 = 1A x 3O = 3V
VR3= I x R3 = 1A x 5O = 5V
اگر این ولتاژها را با هم جمع کنیم، ده ولت برابر با ولتاژ اعمال شده به مدار بدست می آید.
بنابراین، میتوان نتیجه گرفت که کل ولتاژ مدار سری برابر است با مجموع ولتاژهای هر مدار.
Vt= VRx + VRy + VRz+.........+ VRn
مدار تقسیم کننده ولتاژ
در شکل داده شده مداری را می بینید که دارای 2 مقاومت Rx و Ry است که به صورت سری به هم متصل شده اند.
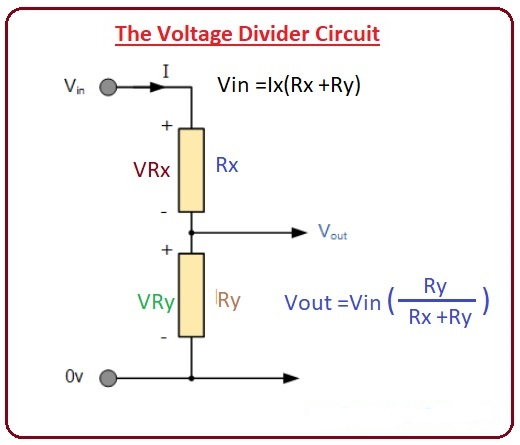
ولتاژ ورودی به یک سر مقاومت Rx و خروجی از دو سر مقاومت Ry گرفته می شود.
مقدار ولتاژ خروجی را می توان با فرمول تقسیم کننده ولتاژ که در زیر آورده شده است پیدا کرد.
Vout = Vin (Ry)/(Rx+Ry)
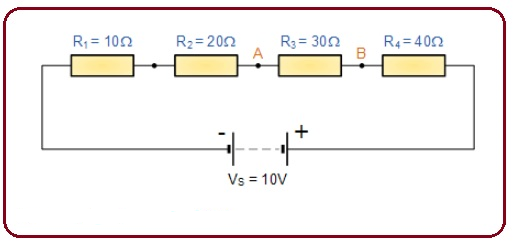
حالا مدارهایی که بیش از 2 مقاومت دارند را حل کنید، در مدار داده شده می بینید که 4 مقاومت وجود دارد و مقادیر آنها نیز ذکر شده است.
اکنون فرمول تقسیم کننده ولتاژ را برای یافتن مقدار ولتاژ در هر مقاومت اعمال می کنیم.

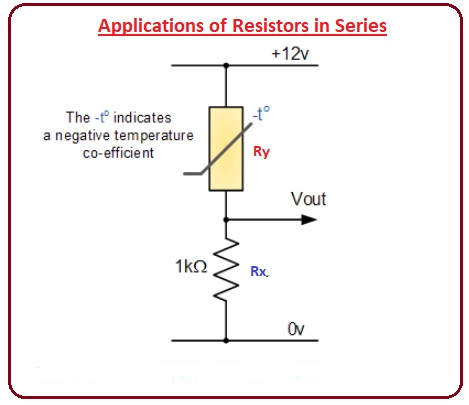
کاربردهای مقاومت ها با آرایش سری شده
مداری را در شکل زیر مشاهده می کنید که شبیه مداری است که در مدار تقسیم کننده ولتاژ بحث کردیم، اما در این مدار مقاومت وابسته به نور وجود دارد، هر کمیت فیزیکی را به سیگنال الکتریکی تبدیل می کند.
فرض کنید مقدار LDR ده کیلو اهم و مقدار مقاومت RX هزار اهم باشد اگر قانون تقسیم کننده ولتاژ را اعمال کنیم.
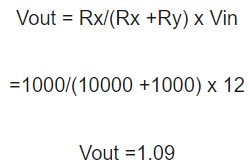



دیدگاه خود را بنویسید