ترکیب موازی مقاومت ها
در این آموزش، در مورد اتصال مقاومت ها به صورت موازی صحبت خواهیم کرد. 2 نوع اتصال اصلی وجود دارد که برای ساخت مدار استفاده می شود. یکی اتصال سری و دومی موازی است. اگر اجزای موجود در مدارها موازی یکدیگر باشند، شاخه های مجزای خود را دارند. این انشعابات مسیرهای متفاوتی را برای جریان فراهم می کنند. در مدارهای موازی، جریان در هر بخش مدار دارای مقدار متفاوتی است و ولتاژ هر قسمت برابر با ولتاژ ورودی است. اکنون نگاهی به مدارهایی خواهیم داشت که دارای مقاومت های موازی هستند و نشان می دهیم که چگونه می توانیم مقاومت معادل مدار و جریان و ولتاژ را در هر یک از آنها پیدا کنیم..
در مدارهای الکتریکی، مقاومت ها به صورت موازی متصل می شوند اگر هر دو نقطه انتهایی آنها به نقاط انتهایی مقاومت یا مقاومت های دیگر متصل شوند.
همانطور که در مدارهای مقاومت سری، یک مسیر برای عبور جریان وجود دارد اما در مدارهای موازی، مسیرهای زیادی برای جریان وجود دارد. به همین دلیل مدارهای موازی به عنوان مدار تقسیم کننده جریان شناخته می شوند.
همانطور که راه های متعددی برای جریان در مدار موازی وجود دارد، بنابراین جریان های متفاوتی در هر قسمت از مدار جریان می یابد. ولتاژ در مقاومت های موازی مدار یکسان خواهد بود.
در مدار زیر 3 مقاومت Rx، Ry، Rz وجود دارد که ولتاژ هر یک از آنها یکسان خواهد بود.
VRx = VRy = VRz = 12 ولت
روش مشخص برای یافتن مقاومت معادل در اتصال موازی از رابطه زیر به دست می آید.
Rt-1= 1/Ra + 1/Rb +1/Rc .....1/Rn
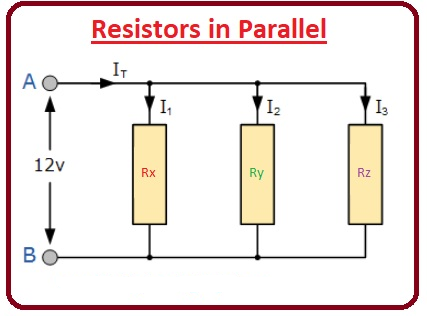
جریان ها در مدار با مقاومت های موازی
جریان خالصی که از مدار مقاومت های موازی می گذرد معادل مجموع جریان هایی است که از هر مقاومت مدار عبور می کنند.
اما جریان در هر شاخه مدار الزاماً مشابه نخواهد بود و بستگی به میزان مقاومت هر شاخه دارد.
به عنوان مثال، از آنجایی که ولتاژ در هر مقاومت موازی مشابه است و به دلیل مقادیر مختلف مقاومت، جریان یکسان نخواهد بود.
اکنون برای درک بهتر بیایید مداری بسازیم که 2 مقاومت موازی داشته باشد، در شکل زیر نشان داده شده است.
اگر قانون جریان Kirchoff را در این مدار نسبت به آنچه که داریم اعمال کنیم، جریان عبوری از هر مقاومت IRx و IRy است.
IT= IRx +IRy
اگر قانون اهم را برای هر دو مقاومت اعمال کنیم، می توانیم جریان عبوری از آنها را پیدا کنیم.
IRx = V/Rx = 12/20 = 0.6A
IRy =V/Ry= 12/47=0.255A
بنابراین کل جریان خواهد بود.
IT=0.255+0.6=0.855 A
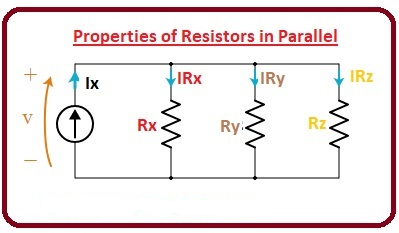
خواص مقاومت های موازی شده
در نمودار داده شده یک مدار مقاومت موازی نشان داده شده است که دارای 3 مقاومت Rx، Ry، Rz به صورت موازی و یک منبع جریان است.
جریان Ix از منبع به 3 مقاومت مدار می رسد و به سه مسیر مختلف تقسیم می شود.
اگر قانون اهم را برای این مدار اعمال کنیم، این عبارت را خواهیم داشت.
Ix=IRx+IRy+IRz
ولتاژ در هر مقاومت یکسان خواهد بود.
VRx = (IRx) . (Rx)
VRy = (IRy) . (Ry)
VRz = (IRz) . (Rz)
اکنون از این مقدار ولتاژ یکسان هر مقاومت استفاده کنید و جریانی را که در آنها جریان دارد پیدا کنید.
IRx = VRx/Rx
IRy = VRy/Ry
IRz = VRz/Rz
اگر این 3 جریان را با هم جمع کنیم مقدار حاصل برابر با جریان منبع فعلی خواهد بود.
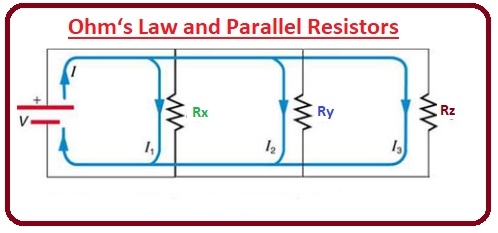
قانون اهم و مقاومت های موازی
برای ارتباط قانون اهم و ترکیب موازی مقاومت ها، مداری را مثال می زنیم که 3 مقاومت متصل به صورت موازی و منبع ولتاژ به آنها متصل شده اند.
ولتاژ هر مقاومت برابر با منبع ولتاژ است. اگر قانون اهم را اعمال کنیم، جریان در هر مقاومت خواهد بود.
I1 =(V)/(Rx)
I2=(V)/(Ry)
I3= (V)/(Rz)
با توجه به اصل بقای بار، کل جریان عبوری در مدار برابر با جریان عبوری از این سه مقاومت خواهد بود.
I = (I1 + I2 +I3)
اگر مقادیر جریان های جاری را در مقاومت 3 قرار دهیم، خواهیم داشت.
I = (V)/(Rx) + (V)/(Ry) + (V)/(Rz)
I =V (1/Rx + 1/Ry + 1/Rz)
از این رابطه می توان نتیجه گرفت که مقاومت کل در مدارهای موازی معادل مجموع معکوس هر مقاومت است.
بنابراین، مقاومت معادل در مدار موازی است.
Rn-1 = 1/Rx + 1/Ry + 1/Rz +.........+1/Rn
کاربردهای مدار با مقاومت های موازی
تقریباً همه خانههای مسکونی از ترکیب موازی برای سیمکشی برق استفاده میکنند، زیرا ما میتوانیم بدون اینکه همه دستگاهها را از مدار خارج کنیم، وسایل خانه را روشن و خاموش کنیم.
در صورت بروز هرگونه اتصال کوتاه در یک دستگاه یا آسیب دیدن آن به دلیل برخی ایرادات الکتریکی، مدار آن دستگاه خاص را جهت رفع عیب قطع می کنیم نه کل مدار را.
مدارهای موازی فقط در خانه های مسکونی استفاده نمی شود بلکه در انتقال و توزیع برق به ساختمان های بزرگ و مناطق مختلف نیز استفاده می شود.
امروزه ایستگاه های شبکه ما بر اساس ترکیب مدارهای موازی طراحی می شوند، زمانی که مدار فیدر قطع می شود، فیدرهای دیگر در شبکه به کار خود ادامه می دهند و نیرو را به بار می رسانند.



دیدگاه خود را بنویسید